Comparing Fractions: Understanding Which is Bigger or Smaller
Understanding how to compare fractions is an essential skill in mathematics that helps learners grasp concepts of quantity, proportion, and value. This page is dedicated to guiding students through the process of comparing fractions, whether they are just starting or looking to refine their skills. Using hands-on activities and real-world applications, we aim to make this learning experience engaging and effective, encouraging critical thinking and curiosity in every learner.
Fractions are a way to represent parts of a whole. When comparing fractions, it’s important to understand how they work. Fractions are made up of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many parts we are talking about.
How to Compare Fractions with the Same Denominator
When two fractions have the same denominator, the larger the numerator, the larger the fraction. For example, if we have the fractions 2/4 and 3/4, both fractions have the same denominator (4). But since 3 is bigger than 2, 3/4 is larger than 2/4. Here's an easy way to see it:
- 2/4 means 2 out of 4 equal parts.
- 3/4 means 3 out of 4 equal parts.
So, if you imagine a pizza divided into 4 slices, 3/4 would be 3 slices out of 4, and 2/4 would be only 2 slices. Clearly, 3/4 is more!
A Simple Picture to Help
Imagine a pizza divided into 4 slices. Here's how to compare 2/4 and 3/4:
2/4: 🍕🍕⬜⬜
3/4: 🍕🍕🍕⬜
In the first pizza, there are only 2 slices out of 4, but in the second pizza, there are 3 slices out of 4. So, 3/4 is the larger fraction because it covers more of the pizza!
Why Is This Important?
Understanding fractions helps us in real life! For example, when you’re baking, you may need to compare how much of an ingredient you have. If a recipe asks for 2/4 cup of sugar and you have 3/4 cup of sugar, you have more than enough to follow the recipe!
References:
- "Fractions: A Basic Introduction" (Edutopia)
- "Understanding Fractions" (National Council of Teachers of Mathematics)

What Are Fractions?
Fractions represent parts of a whole and are written in the form of one number over another, separated by a line. The number on top is called the numerator, indicating how many parts we have, while the number on the bottom is the denominator, showing how many equal parts the whole is divided into. For example, in the fraction 3/4, we have three parts out of a total of four. Understanding this basic structure is crucial for learners as they move into comparing fractions. To compare fractions effectively, it’s important to have a solid comprehension of numerators and denominators, as well as how they relate to one another. Additionally, recognizing that not all fractions are comparable at a glance emphasizes the need for specific methods and strategies for comparison.
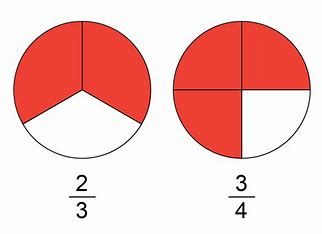
Methods for Comparing Fractions
There are several methods for comparing fractions, and the appropriate technique can depend on the specific fractions involved. One common method is to convert fractions to have a common denominator, which allows for a straightforward comparison. For instance, if we want to compare 1/2 and 3/4, we can convert both fractions to have a denominator of 4; thus, 1/2 becomes 2/4. This way, it's easier to see that 3/4 is larger than 2/4. Another method involves converting fractions to decimals. For example, 1/2 equals 0.5, while 3/4 equals 0.75, clearly displaying that 3/4 is greater. By employing these methods, learners can develop a reliable toolkit for evaluating fractions, which can be applied in various situations, from cooking to budgeting, enhancing their real-world understanding of mathematics.

Hands-On Activities for Mastering Fraction Comparison
At Innovate with Mr. Barbado, we believe in the power of hands-on learning. Engaging activities can help solidify the concepts of comparing fractions in a fun and interactive way. For instance, using fraction tiles or pie charts can visually demonstrate how different fractions relate to one another. Students can manipulate these tools to compare sizes directly and see the impact of changing numerators and denominators. Additionally, practical applications, such as measuring ingredients in cooking or comparing lengths in DIY projects, allow learners to see fractions in action. By incorporating these hands-on experiences into our workshops and tutoring sessions, we foster an engaging environment where students feel empowered to explore and understand the world of fractions, ultimately building their confidence in math.
Ready to Dive Deeper into fraction?
Download the following resources below.
Comparing fractions with the same denominator Lesson Plan.pdf
Comparing Fractions Understanding Which is Bigger or Smaller Article.pdf
Comparing Fractions Project Guide .pdf